Die numerische Simulation physikalischer Phänomene setzt die Kenntnis von Materialparametern voraus. In der Realität zeigt sich jedoch, dass Parameter teilweise unbekannt sind, diese geschätzt oder in Analogie zu Literaturangaben übernommen werden müssen.
Sofort drängt sich die Frage auf, wie groß ist der Einfluss der geschätzten oder übernommenen Parameter auf das Modellergebnis? Wie sensibel reagiert das Ergebnis auf Unschärfen dieses Parameters?
Das Uncertainty Quantification Module von COMSOL Multiphysics® bietet die Möglichkeit, die Auswirkungen von Modellunsicherheiten zu analysieren. Es wird untersucht, wie die Größen von Interesse von Variationen ausgewählter Eingabeparameter beeinflusst werden. Das Uncertainty Quantification Module unterstützt die Methoden Screening, Sensitivitätsanalyse, Unsicherheitsfortpflanzung und Zuverlässigkeitsanalyse.
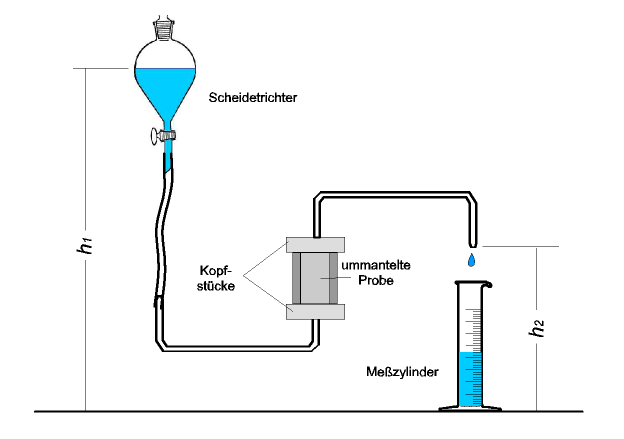
Ein einfaches Beispiel soll den Sachverhalt verdeutlichen. Die Durchströmung eines porösen Körpers wird mit Hilfe des Darcy-Gesetzes beschrieben. Der dafür erforderliche Materialparameter ist der Durchlässigkeitsbeiwert, der im einfachsten Fall durch einen Versuch direkt bestimmt werden kann.
Abbildung 1 zeigt den Versuchsaufbau (Werner Muck, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10336325). Der Durchlässigkeitsbeiwert kann für die stationäre Strömung berechnet werden:
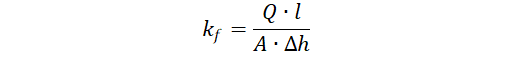
Für die Simulation des Stofftransports im porösen Körper werden zusätzlich die Porosität sowie die longitudinale und transversale Dispersivität benötigt, deren Bestimmung aufwendiger ist. Welcher Parameter kann geschätzt und welcher sollte mit Hilfe von Messwerten aus Laborversuchen bestimmt werden?
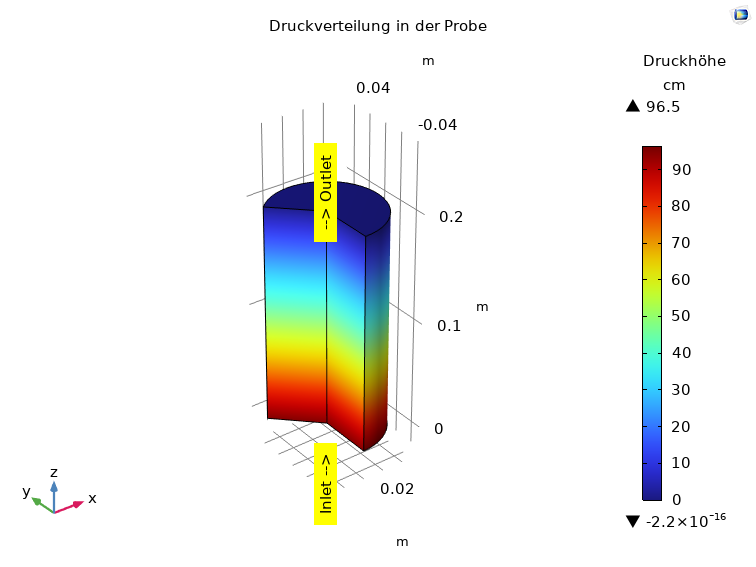
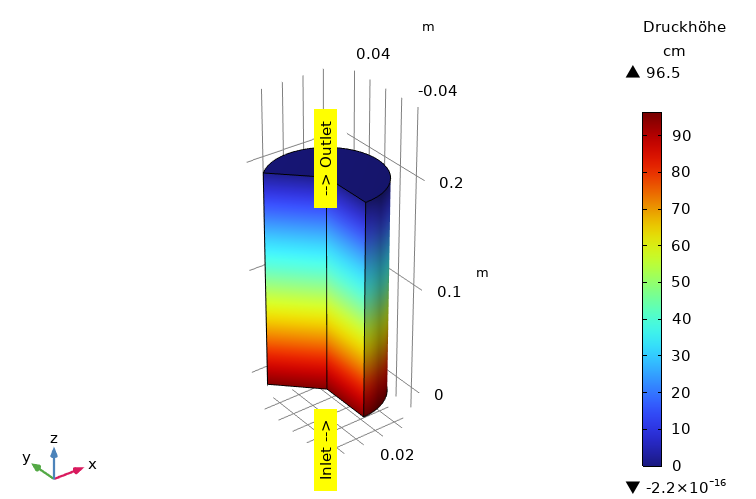
Erforderliche Antworten gibt die Unsicherheitsanalyse. Mit einem Simulationsmodell der Durchströmung eines zylindrischen porösen Körpers in Anlehnung an den oben gezeigten Versuch wird die Darcy-Strömung mit dem Transport eines idealen Tracers auf der Grundlage des ermittelten Durchlässigkeitsbeiwertes und der geschätzten Parameter Porosität und Dispersivität gerechnet (Abbildung 2). Von Interesse ist der Durchgang der Stofffront eines idealen Tracers am Outlet der Probe, variiert werden Porosität und Dispersivität.
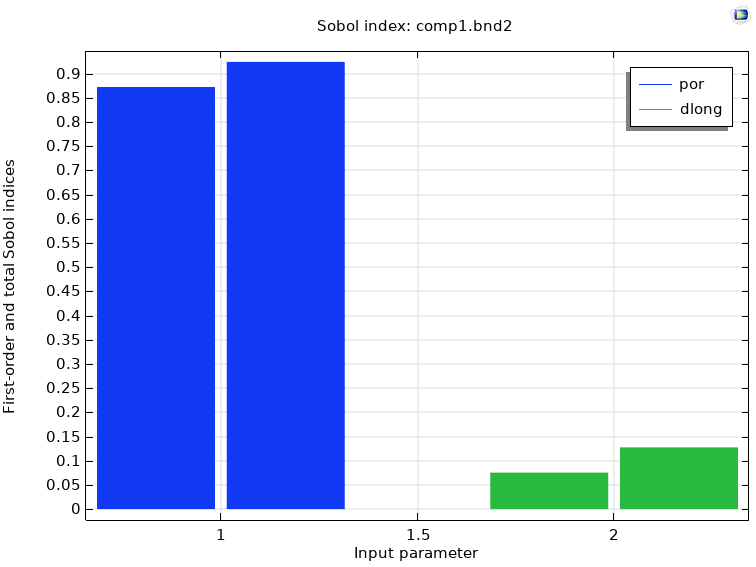
Mit Hilfe der Sensitivitätsanalyse kann der SOBOL-Index für jeden Parameter ermittelt werden. Abbildung 3 zeigt, dass die Porosität por einen wesentlich größeren Einfluss auf den Durchgang der Stofffront hat als die Dispersivität dlong.
Die Screening-Methode ermittelt den MOAT-Mittelwert und die MOAT-Standardabweichung für die Eingabeparameter Porosität und Dispersivität (Abbildung 4). Ein hoher MOAT-Mittelwert für den Parameter Porosität zeigt, dass die Porosität einen signifikanten Einfluss auf den Durchgang der Stofffront hat. Für den Parameter Dispersivität berechnet die Analyse einen geringen MOAT-Mittelwert bei einer hohen MOAT-Standardabweichung. Dies bedeutet, dass der direkte Einfluss des Parameters geringer ist, er aber stark mit der Porosität interagiert. Da sich die Abstandsgeschwindigkeit indirekt proportional zur Porosität verhält und die Abstandsgeschwindigkeit auch in den dispersiven Massenfluss eingeht, ist das Ergebnis nachvollziehbar.
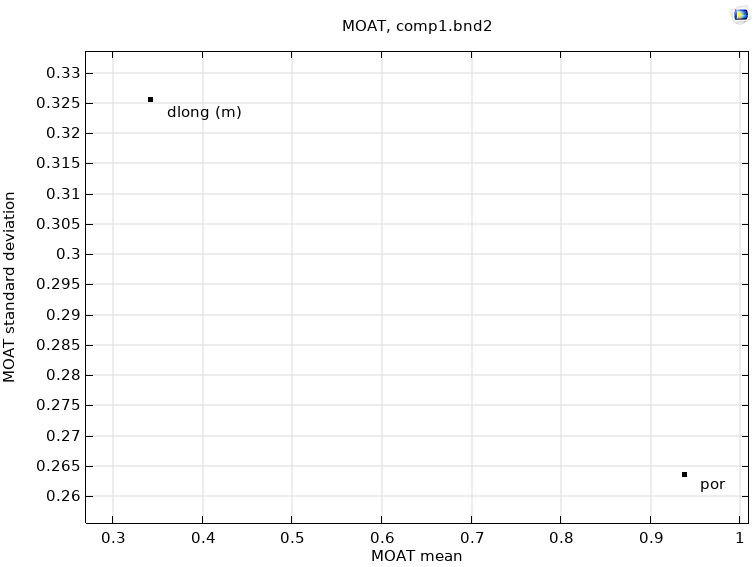
Fazit der Analyse ist, dass der Ermittlung des Parameters Porosität mehr Aufmerksamkeit gewidmet werden sollte als der des Parameters Dispersivität. Die Porosität hat einen größeren Einfluss auf den Durchgang der Stofffront. Diese Erkenntnis hat eine hohe praktische Bedeutung, da Versuche zur Ermittlung von Parametern Zeit und Geld kosten.
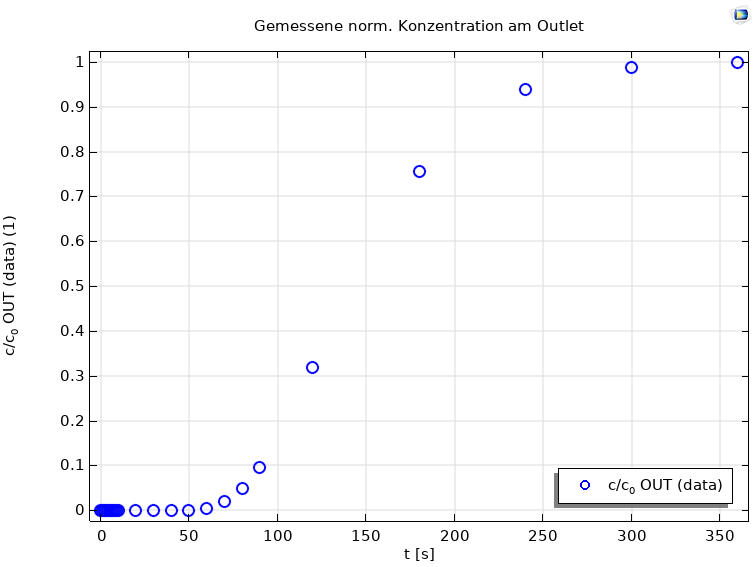
Für die Ermittlung der Porosität wurde der Transport eines idealen Tracers beobachtet. Abbildung 5 zeigt die gemessenen normierten Konzentrationen für den Durchgang der Stofffront am Outlet des zylindrischen Probekörpers.
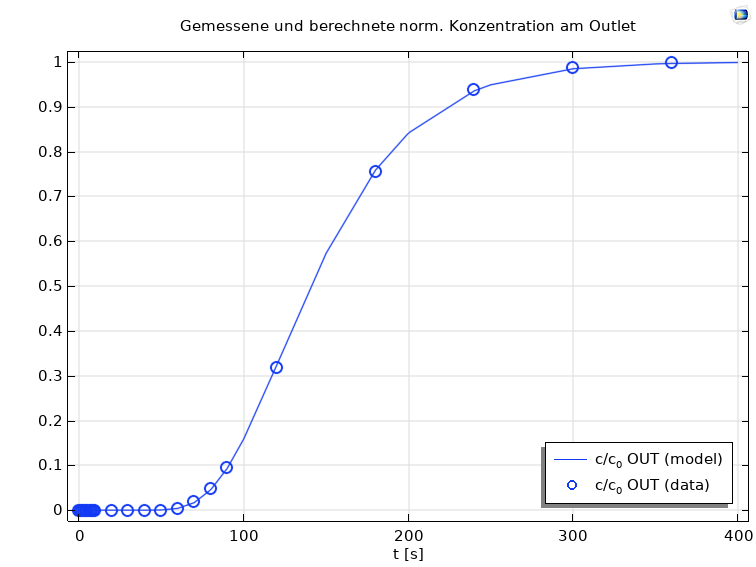
Mit Hilfe der Parameterschätzungsfunktion (Parameteridentifikation) von COMSOL Multiphysics® wurden mit dem Simulationsmodell die Parameter Porosität und Dispersivität auf Basis der Messwerte ermittelt. Ausgehend von den Startparametern Porosität=0.2 und Dispersivität=0.01m wurden die zutreffenden Parameter Porosität=0.1 und Dispersivität=0.0145m identifiziert. Nachfolgende Abbildung zeigt die gemessenen und berechneten normierten Konzentrationen am Outlet der zylindrischen Probe.
Die Unsicherheitsanalyse und die Parameteridentifikation sind zwei starke Player bei der numerischen Simulation mit einem hohen Nutzwert. Was exemplarisch an einem sehr einfachen Beispiel gezeigt wurde, lässt sich für beliebige Prozesse und Physiken formulieren. Die Unsicherheitsanalyse hilft, die Vertrauenswürdigkeit des Ergebnisses einzuschätzen und zu priorisieren, welche Parameter genauer bestimmte werden sollten. Dadurch sind die Unsicherheitsanalyse und die Parameteridentifikation zwei bedeutsame Werkzeuge, um eine Simulationsaufgabe mit der erforderlichen Parameterbeschaffung wirtschaftlich und effizient gestalten zu können.
Sollten Sie Fragen zu diesem interessanten Thema haben, können Sie uns gerne kontaktieren.